Phylogenetic beta diversity • phylospatial

This vignette covers topics related to phylogenetic beta diversity, including calculation of pairwise dissimilarity between sites, and use of these dissimilarity values in ordination and regionalization analyses.

To get started, let’s load the phylospatial library, as well as tmap for visualization. Note that the functions covered here all require a phylospatial object as input; see vignette("phylospatial-data") for details on constructing data sets. We’ll use the moss() example data here.

library(phylospatial); library(tmap); library(magrittr)
ps <- moss()

Dissimilarity

The phylospatial package provides a range of methods for calculating pairwise community phylogenetic distances among locations. It can calculate phylogenetic versions of any quantitative community dissimilarity metric available trough the vegan package, including the various predefined indices provided through vegan::vegdist as well as custom indices specified through vegan::designdist. The default metric is Bray-Curtis distance, also known as quantitative Sorensen’s dissimilarity. Additional choices allow for partitioning dissimilarity in to turnover and nestedness components.

Dissimilarity is computed using the function ps_add_dissim(), which adds a distance matrix to the dissim slot of your phylospatial data set. Or if you just want the matrix itself, you can use ps_dissim().

In addition to specifying the dissimilarity index to use, these functions include options for different ways to scale the phylogenetic community matrix before calculating dissimilarity. Setting endemism = TRUE will scale every lineage’s occurrence values to sum to 1 across all sites, giving greater weight to narrowly distributed taxa. Setting normalize = TRUE scales every site’s total occurrence value to sum to 1 across taxa, which results in a distance matrix that emphasizes proportional differences in composition rather than alpha diversity gradients.

Let’s run an example using quantitative Sorensen’s index, weighted by endemism. Printing the result, we can see it now contains dissimilarity data; this is a square distance matrix with a row and column for each site:

ps <- ps_add_dissim(ps, method = "sorensen", endemism = TRUE, normalize = TRUE)
ps
#> `phylospatial` object
#>   - 884 lineages across 527 occupied sites (1116 total) 
#>   - community data type: probability 
#>   - branch length rescaling: sum1 
#>   - spatial data class: SpatRaster 
#>   - dissimilarity data: sorensen

Distance decay

One frequent use of dissimilarity matrices is to analyze how commmunity phylogentic similarity declines with geographic distance, environmental difference, or other geographic properties. Common methods for this kind of analysis include generalized dissimilarity modeling and partial Mantel tests.

Here let’s just visualize how phylogenetic turnover changes with the distance between sites. We can compute a pairwise geographic distance matrix using ps_geodist(). Let’s also compare this to non-phylogenetic species turnover, which we can compute by specifying tips_only = TRUE. We can summarize the pattern with a LOESS curve:

phy_beta <- as.vector(ps_dissim(ps, method = "sorensen"))
spp_beta <- as.vector(ps_dissim(ps, method = "sorensen", tips_only = TRUE))
geo_dist <- as.vector(ps_geodist(ps)) / 1000  # convert to km

# subsample for plotting (full pairwise set is huge)
ss <- sample(length(phy_beta), 5000)

plot(geo_dist[ss], phy_beta[ss],
     pch = ".", col = adjustcolor("steelblue", 0.3),
     xlab = "Geographic distance (km)",
     ylab = "Dissimilarity",
     ylim = c(0, 1))
points(geo_dist[ss], spp_beta[ss],
       pch = ".", col = adjustcolor("tomato", 0.3))
 
# loess trend lines
lo_phy <- loess(phy_beta[ss] ~ geo_dist[ss])
lo_spp <- loess(spp_beta[ss] ~ geo_dist[ss])
ox <- order(geo_dist[ss])
lines(geo_dist[ss][ox], predict(lo_phy)[ox], col = "steelblue", lwd = 2)
lines(geo_dist[ss][ox], predict(lo_spp)[ox], col = "tomato", lwd = 2)
 
legend("bottomright",
       legend = c("Phylogenetic", "Species"),
       col = c("steelblue", "tomato"),
       lwd = 2, bty = "n")

Ordination

Additional approaches for assessing spatial turnover patterns include ordination or clustering, both of which reduce a dissimilarity matrix into a lower-dimensional summary. Ordination, which is implemented in the function ps_ordinate(), identifies the dominant axes of variation in phylogenetic turnover, which can then be used for visualization or analysis. The funtion offers various ordination methods. Let’s perform a PCA, and make maps of the first four dimensions:

ps %>%
      ps_ordinate(method = "pca", k = 4) %>%
      tm_shape() +
      tm_raster(col.scale = tm_scale_continuous(values = "brewer.pi_yg"),
                col.free = FALSE) +
      tm_title("Phylogenetic community ordination")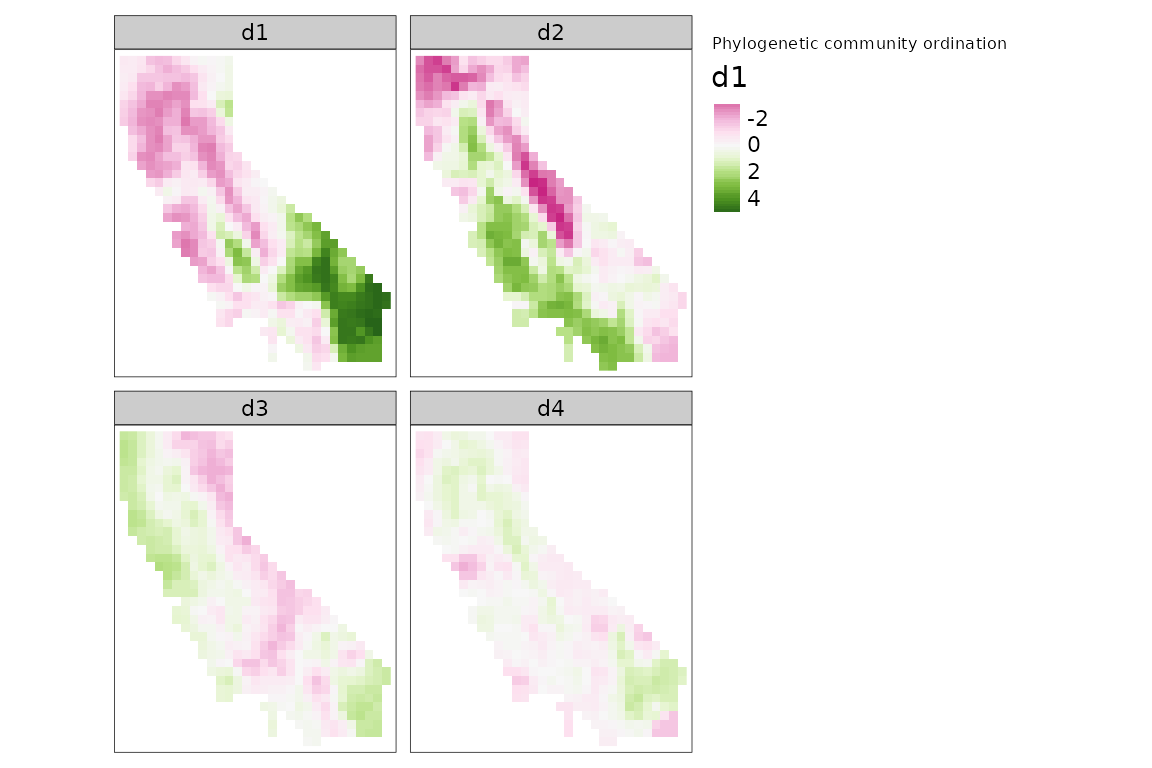

We can also qualitatively visualize compositional patterns by converting ordination axes to a set of colors representing how similar two sites are to each other, using the ps_rgb() function. Let’s do that here, using the "cmds" (classical multidimensional scaling) ordination algorithm, and then plot the result using tmap::tm_rgb():

ps %>%
      ps_rgb(method = "cmds") %>%
      tm_shape() +
      tm_rgb(col.scale = tm_scale_rgb(max_color_value = 1), 
             interpolate = FALSE) +
      tm_title("Phylogenetic community ordination")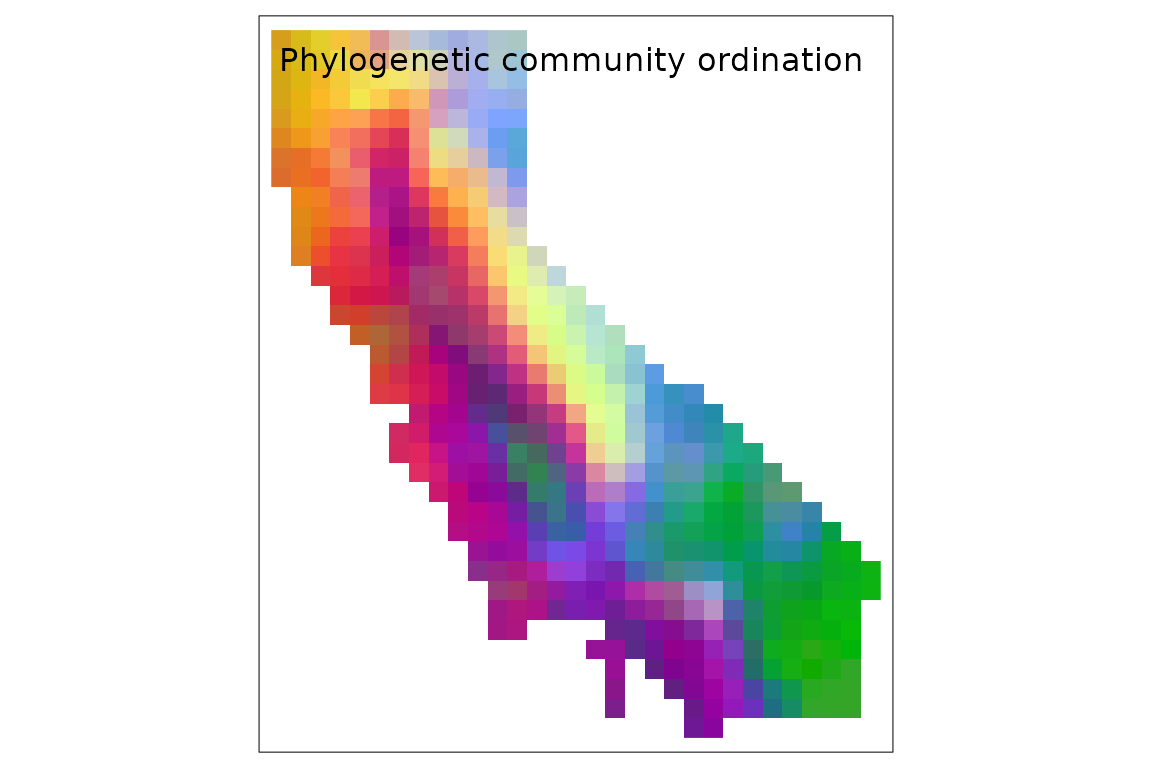

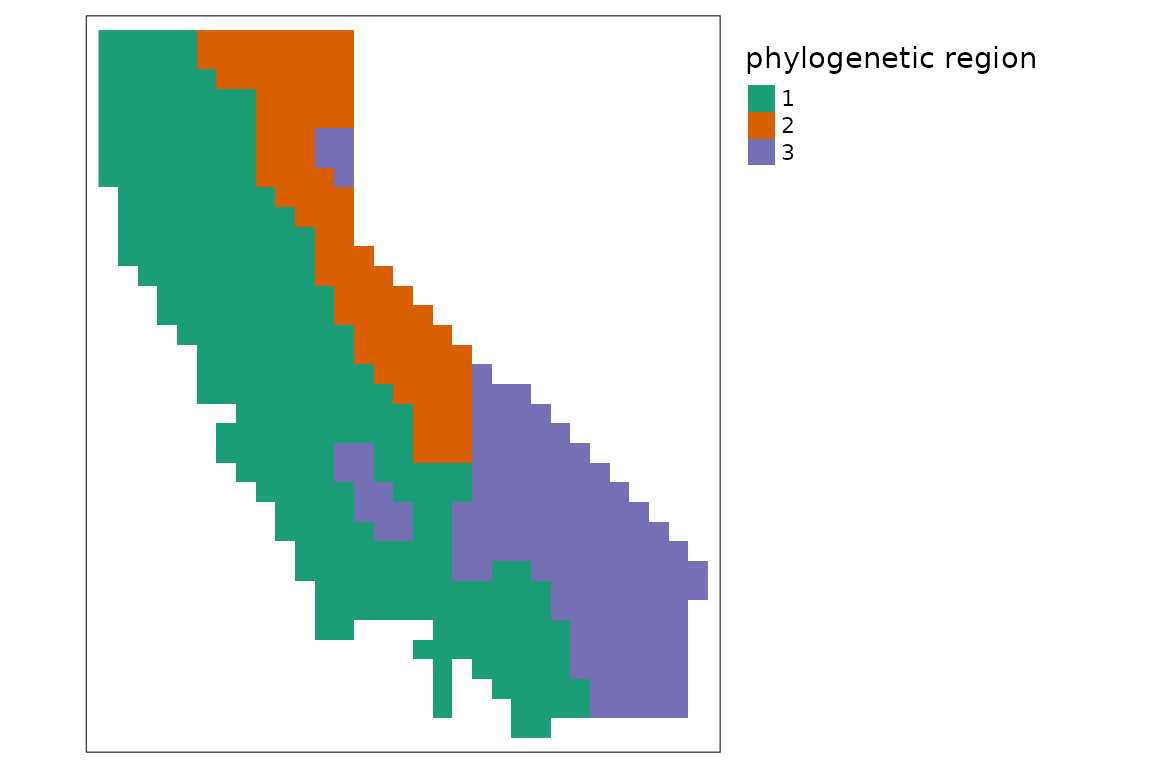
Regionalization

We can also perform a more formal cluster analysis that splits the landscape into a set of evolutionary bioregions, using the ps_regions() function. To do this, we need to specify the clustering method and the number of clusters (k). Choices of method include k-means and various hierarchical clustering methods; note that results are sometimes highly sensitive to which method is selected. The hierarchical methods require a dissimilarity matrix calculated by first running ps_add_dissim(), while k-means does not.

Choosing k is usually subjective. Many alternative methods have been proposed in the literature to identify the “optimal” number of clusters in a data set, but ecological data are often inherently characterized by continuous gradients rather than discrete provinces, in which case no value of k may clearly fit best. You can use the function ps_regions_eval() to help evaluate how well different choices for k fit the data by comparing the variance explained by different numbers of clusters. Let’s do that here, using the "average" hierarchical clustering method:

ps_regions_eval(ps, k = 1:15, plot = TRUE, method = "average")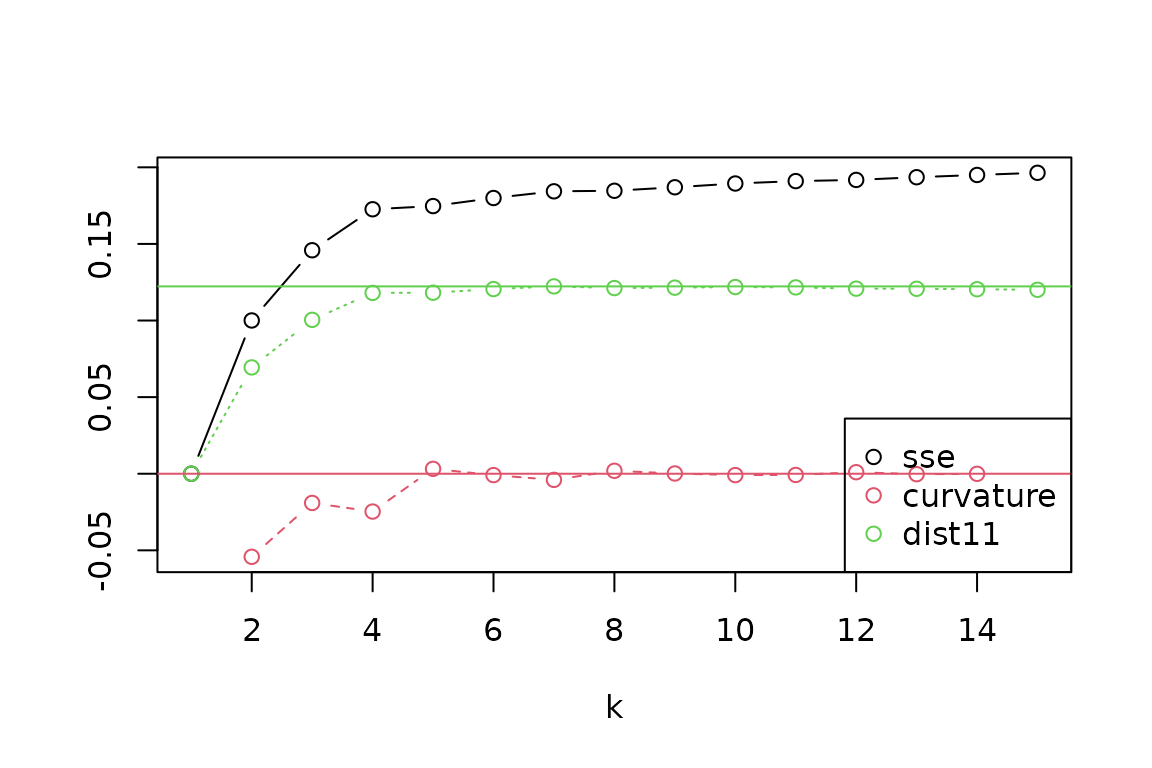

From the evaluation plot, it looks like a value of k = 4 stands out as the most distinct “elbow” in explained variance (“SSE”), with near-maximum distance to the 1:1 line (“dist11”), and with more negative “curvature” than its neighbors, though other choices could also be reasonable. Let’s generate results for four regions, and then make a map of these zones:

ps %>%
      ps_regions(k = 4, method = "average") %>%
      tm_shape() +
      tm_raster(col.scale = tm_scale_categorical(values = "brewer.dark2"),
                col.legend = tm_legend(show = FALSE)) +
      tm_title("phylogenetic region")