Skip to contents

Suggest a reasonable n_iter for a randomization

Source: R/suggest_n_iter.R
suggest_n_iter.Rd

Uses trace diagnostics to estimate how many burn-in iterations are needed for a nullcat or quantize randomization to reach its apparent stationary distribution, given a dataset and randomization method. Uses a "first pre-tail sign-crossing" rule per chain, then returns the maximum across chains. Can be called on a community matrix or a cat_trace object.

Usage

suggest_n_iter(trace = NULL, tail_frac = 0.3, plot = FALSE, ...)

Arguments

trace

Either a cat_trace object (as returned by trace_cat()), or NULL. If NULL, arguments to trace_cat(), including x and any other relevant parameters must be supplied via ...

tail_frac

Fraction of the trace (at the end) used as the tail window (default 0.3).

plot

If TRUE, plot the trace, with a vertical line at the suggested value.

...

Arguments passed to trace_cat() including arguments it passes to the nullcat() or quantize() function. Ignored if trace is non-NULL.

Value

An integer of class "nullcat_n_iter" with attributes: n_iter (numeric or NA), trace (matrix), steps (vector), tail_mean (per-chain), per_chain (data.frame), converged (logical).

Details

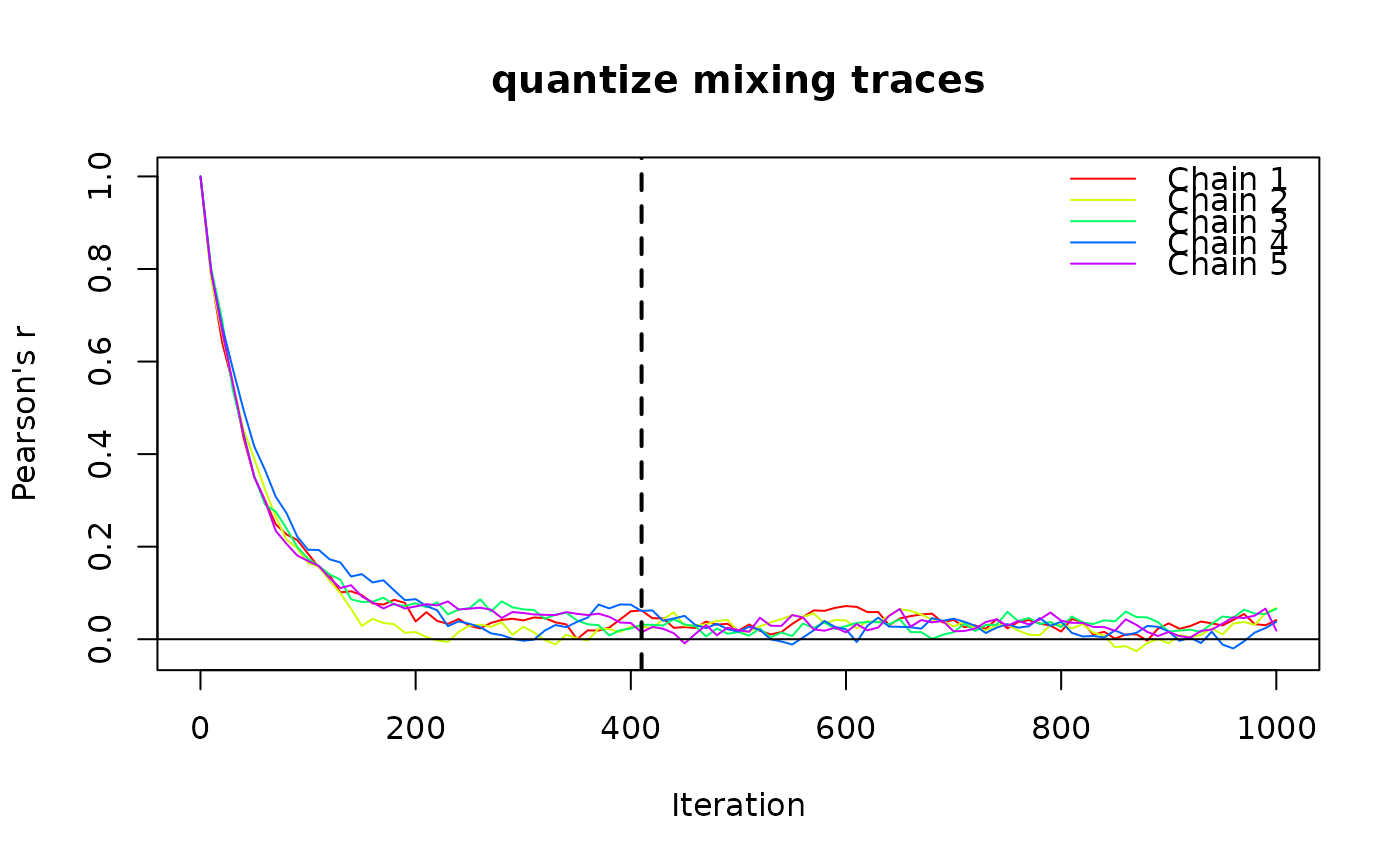
This function uses a “first pre-tail sign-crossing” heuristic to identify burn-in cutoff. This is a simple variant of standard mean-stability tests used in MCMC convergence diagnostics (e.g., Heidelberger & Welch 1983; Geweke 1992; Geyer 1992). It computes the long-run mean based on the "tail window" of the chain, and detects the first iteration at which the trace statistic crosses this long-run mean, indicating that the chain has begun to oscillate around its stationary value. If the chain does not reach the long-run mean before the start of the tail window, the chain is determined not to have reached stationarity, and the function returns NA with attribute converged = FALSE.

References

Heidelberger, P. & Welch, P.D. (1983). Simulation run length control in the presence of an initial transient. Operations Research, 31(6): 1109–1144.

Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. In Bayesian Statistics 4, pp. 169–193.

Geyer, C.J. (1992). Practical Markov Chain Monte Carlo. Statistical Science, 7(4): 473–483.

Feller, W. (1968). An Introduction to Probability Theory and Its Applications, Vol. I. Wiley.

Examples

set.seed(1234)
x <- matrix(sample(1:5, 2500, replace = TRUE), 50)

# call `trace_cat`, then pass result to `suggest_n_iter`:
trace <- trace_cat(x = x, fun = "nullcat", n_iter = 1000,
                     n_chains = 5, method = "curvecat")
suggest_n_iter(trace, tail_frac = 0.3, plot = TRUE)

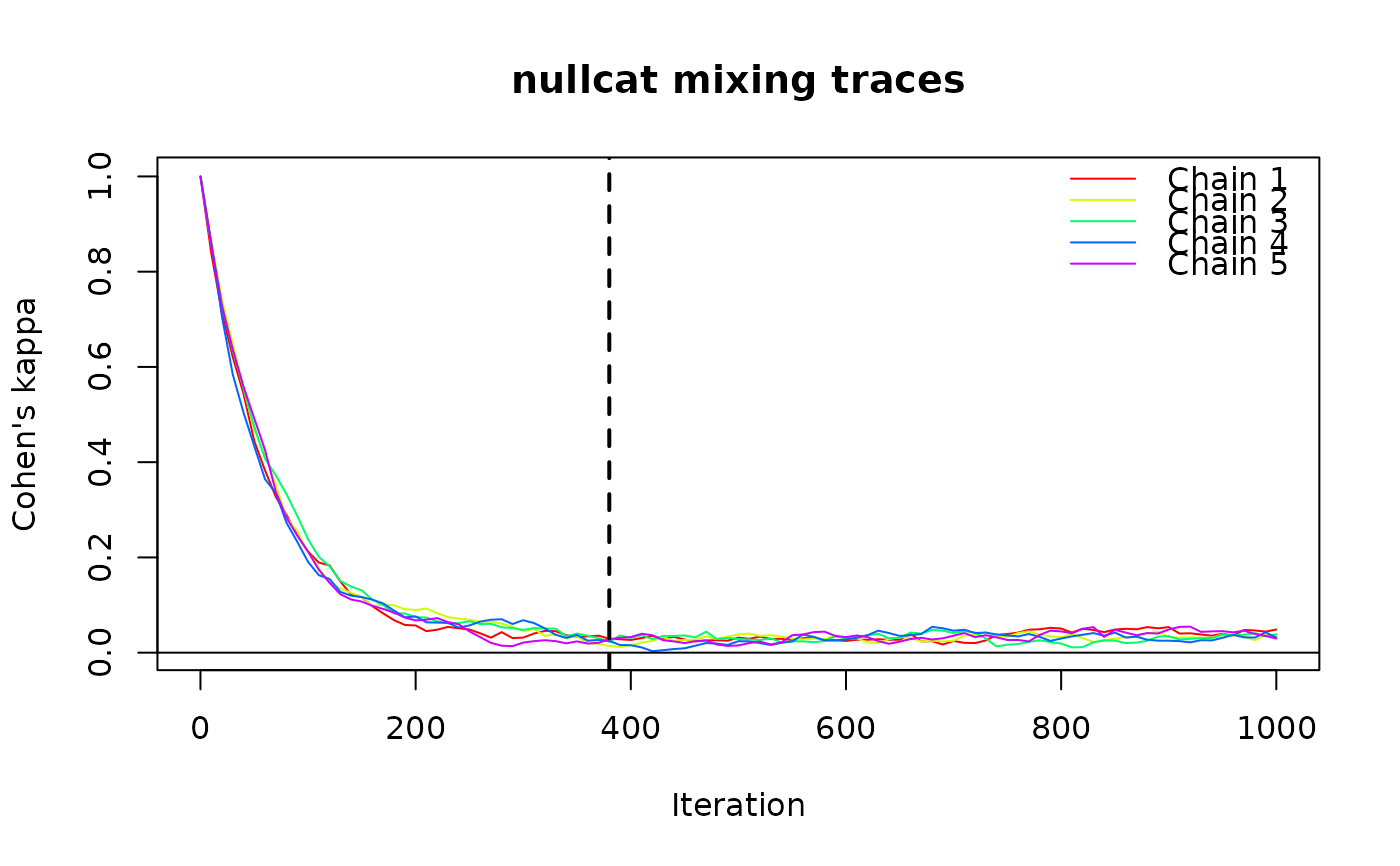#> suggested_n_iter object
#> -----------------------
#> Converged: TRUE 
#> Suggested n iterations: 380 

# alternatively, supply `trace_cat` arguments directly to `suggest_n_iter`:
x <- matrix(runif(2500), 50)
n_iter <- suggest_n_iter(
    x = x, n_chains = 5, n_iter = 1000, tail_frac = 0.3,
    fun = "quantize", n_strata = 4, fixed = "stratum",
    method = "curvecat", plot = TRUE)